Mateusz BOGDAN

Logo

My personal site, with a short presentation of who I am, my academic and professional activities and research interests !

Home
About Me
Research
Publications
Teachings
Datavisualisation
Code
Inspirations - Links

Code snippets

-

Some useful tricks and hacks I use frequently, mostly in Python.

Python Basics

All my code snippets, my sort of personal cheet sheat, has been moved to this web site (in French), which I am developing as part of my teaching activities (work in progress). It is intended for students and covers Python fundamentals as well as practical dataframe tips.

Learn Python

[In French] Python fundamentals, for Basics, NumPy, Pandas and Visualization

Python-Lab

[In French] Interactive notebooks that cover all sections of Learn Python !

Maps and GIS related questions

Recently I’ve ben working with maps in python applications. I mostly use geopandas, dash-leaflet, plotly.scattermapbox, etc.

Distance between two points on a sphere

Compute the distance in km (or meters) between 2 points of the globe defined by their respective lat / lon.

Moving on a sphere

Miscellaneous Functions

Daylength computation

What is the length of the day in hours ?

I needed to compute the length of days for a complete year, and I started using python libraries like pvlib with its module solarposition() or suntime to get the hours of sunset and sunrise. I kept looking for other solutions as I wanted to avoid dependancies, and i found a post on stackoverflow which gives you exactly that.

It is based on a paper by [Forsytthe et al., 1995], named A Model Comparison for Daylength as a Function of Latitude and Day of Year. It uses only the day_of_year and latitude and returns the length of the day in hours (and even have different definitions for the length of a day).

Usefully, one can provide a list of days of the year (or rather an np.array), and the function will return an array of the same length with daylengths :

def day_length(J, L):
    """
    -----------------------------------------------------------------------------------------
    Based upon : "A model comparison for daylength as a function of latitude and day of year"
    Forsythe et al., 1995, Ecological Modelling 80 (1995) 87-95
    -----------------------------------------------------------------------------------------
    Parameters
    ----------
    J: int / list of int / array 
        day of the year.
    L: float 
        latitude (in °)

    Returns
    -------
    Lenght of the day(s) in hours
    
    To account for various definitions of daylength, modify the "p" value accordingly.
    * Sunrise/Sunset is when the center of the sun is even with the horizon 
    p = 0
    * Sunrise/Sunset is when the top of the sun is even with horizon
    p = 0.26667
    * Sunrise/Sunset is when the top of the sun is apparently even with horizon
    p = 0.8333

    """
    p = 0.8333
    phi = np.arcsin(
            0.39795 * ( np.cos( 0.2163108 + 2 * np.arctan( 0.9671396 * np.tan( 0.00860 * (J-186) ) ) ) )
        )
    D = 24 - (24/np.pi)*np.arccos(
              ( np.sin( p*np.pi/180 ) + np.sin( L*np.pi/180 ) * np.sin( phi ) ) / (np.cos(L*np.pi/180) * np.cos( phi ) )
        )

    return D

Solar declination from day of year

Solar declination is the tilt of the sun relative to Earth’s equator, varying from −23.44° to +23.44° through the year With a widely used approximation, the computation is pretty straight forward !

import numpy as np

def solar_declination(day_of_year):
    """
    Approximate solar declination angle (degrees).

    Parameters
    ----------
    day_of_year : int or array-like
        Day of year (1–365)

    Returns
    -------
    float or ndarray
        Solar declination angle in degrees
    """
    return 23.44 * np.sin(2 * np.pi * (day_of_year - 81) / 365)

Shoelace formula : polygon area

import numpy as np

def polygon_area(vertices: np.ndarray, signed: bool = False) -> float:
    """
    Compute the area of a 2D polygon using the shoelace formula.

    Parameters
    ----------
    vertices : (n, 2) ndarray
        Polygon vertices in order (clockwise or counterclockwise).
        The polygon is assumed closed implicitly.
    signed : bool, default=False
        If True, return the signed area.
        If False, return the absolute area.

    Returns
    -------
    float
        Polygon area.
    """
    vertices = np.asarray(vertices, dtype=float)

    if vertices.ndim != 2 or vertices.shape[1] != 2:
        raise ValueError("vertices must have shape (n, 2)")
    if len(vertices) < 3:
        raise ValueError("a polygon needs at least 3 vertices")

    x = vertices[:, 0]
    y = vertices[:, 1]

    area = 0.5 * np.sum(x * np.roll(y, -1) - y * np.roll(x, -1))
    return area if signed else abs(area)

Basic example:

square = np.array([
    [0.0, 0.0],
    [1.0, 0.0],
    [1.0, 1.0],
    [0.0, 1.0],
])

print(polygon_area(square))          # 1.0
print(polygon_area(square, signed=True))

Why it is elegant ? It is:

Signed area If the vertices are:

That can be useful for checking orientation.

Performance

Pairwise distance matrix

Useful for geometry but also clustering, nearest-neighbor precomputation, and many numerical workflows.

import numpy as np
def pairwise_distance_matrix(X: np.ndarray) -> np.ndarray:
    """
    Compute the full pairwise Euclidean distance matrix.

    Parameters
    ----------
    X : (n, d) ndarray
        Array of n points in d dimensions.

    Returns
    -------
    D : (n, n) ndarray
        Pairwise Euclidean distance matrix.
    """
    X = np.asarray(X, dtype=float)
    diff = X[:, None, :] - X[None, :, :]
    return np.sqrt(np.sum(diff**2, axis=-1))

Basic example:

pts = np.array([
    [0.0, 0.0],
    [1.0, 0.0],
    [1.0, 1.0],
])

D = pairwise_distance_matrix(pts)
print(D)

Why it is elegant ? It uses NumPy broadcasting instead of explicit Python loops:

This is compact and usually much faster than nested Python loops for moderate sizes.

Note: For very large n, this allocates an (n, n, d) array, which can be expensive in memory.

Cache expensive computations

Very useful when the same deterministic function is called repeatedly with identical arguments.

from functools import lru_cache

@lru_cache(maxsize=None)
def expensive_function(n: int) -> int:
    """
    Example of a cached pure function.

    Parameters
    ----------
    n : int
        Input integer.

    Returns
    -------
    int
        Sum of squares from 0 to n-1.
    """
    print(f"Computing for n={n}...")
    return sum(i * i for i in range(n))

Basic example:

print(expensive_function(10_000))
print(expensive_function(10_000))  # returned instantly from cache

Why it is elegant ? @lru_cache gives you memoization in one line.

It works best when:

Typical uses:

Important limitation: arguments must be hashable. So plain lists or NumPy arrays cannot be used directly as cache keys unless converted.

Web developments

I also contribute to bridging research and practice through web applications and digital tools.

National railway ridership map

Access
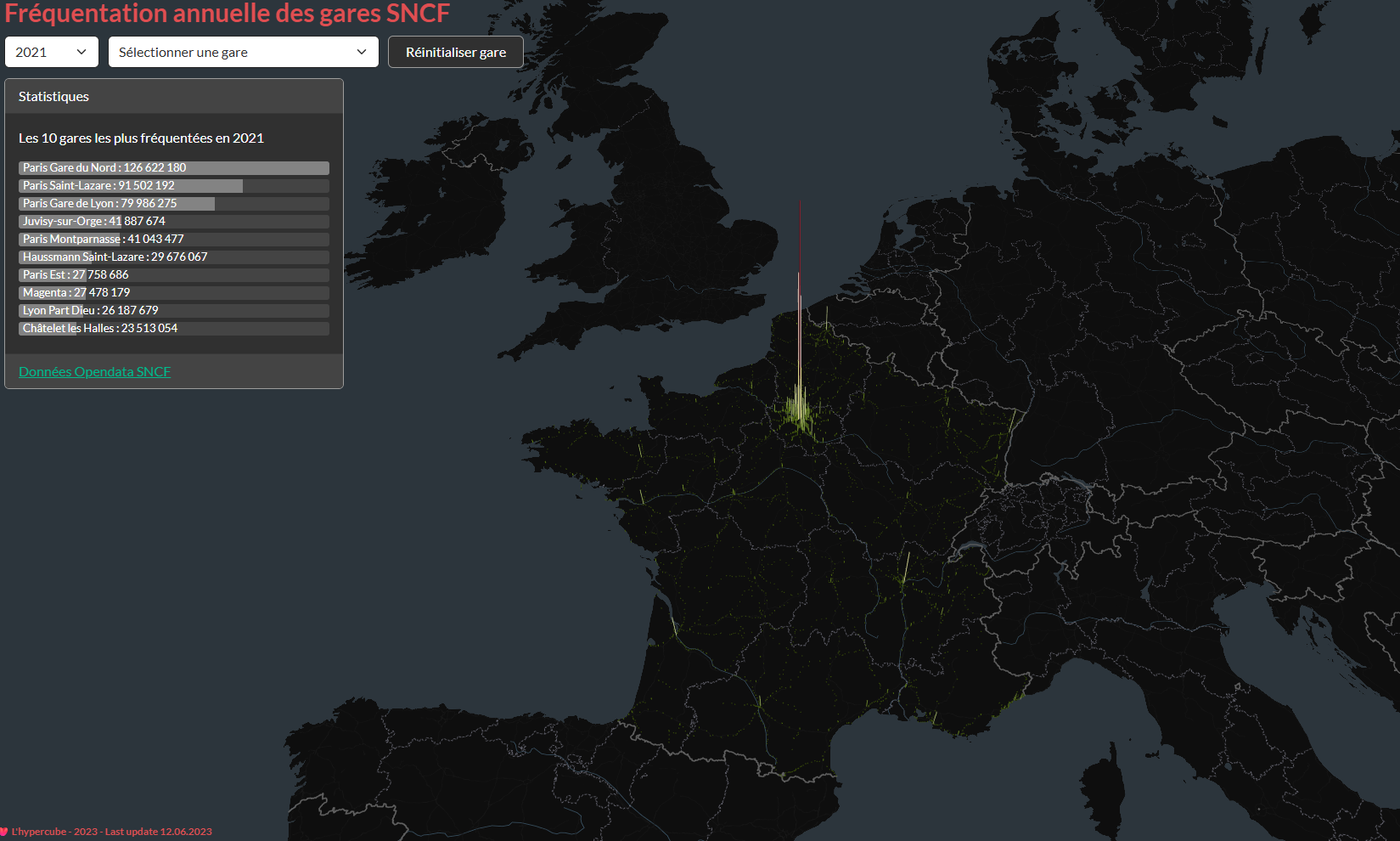
Frequ_nat_sncf

Parisian railway network ridership map and analysis

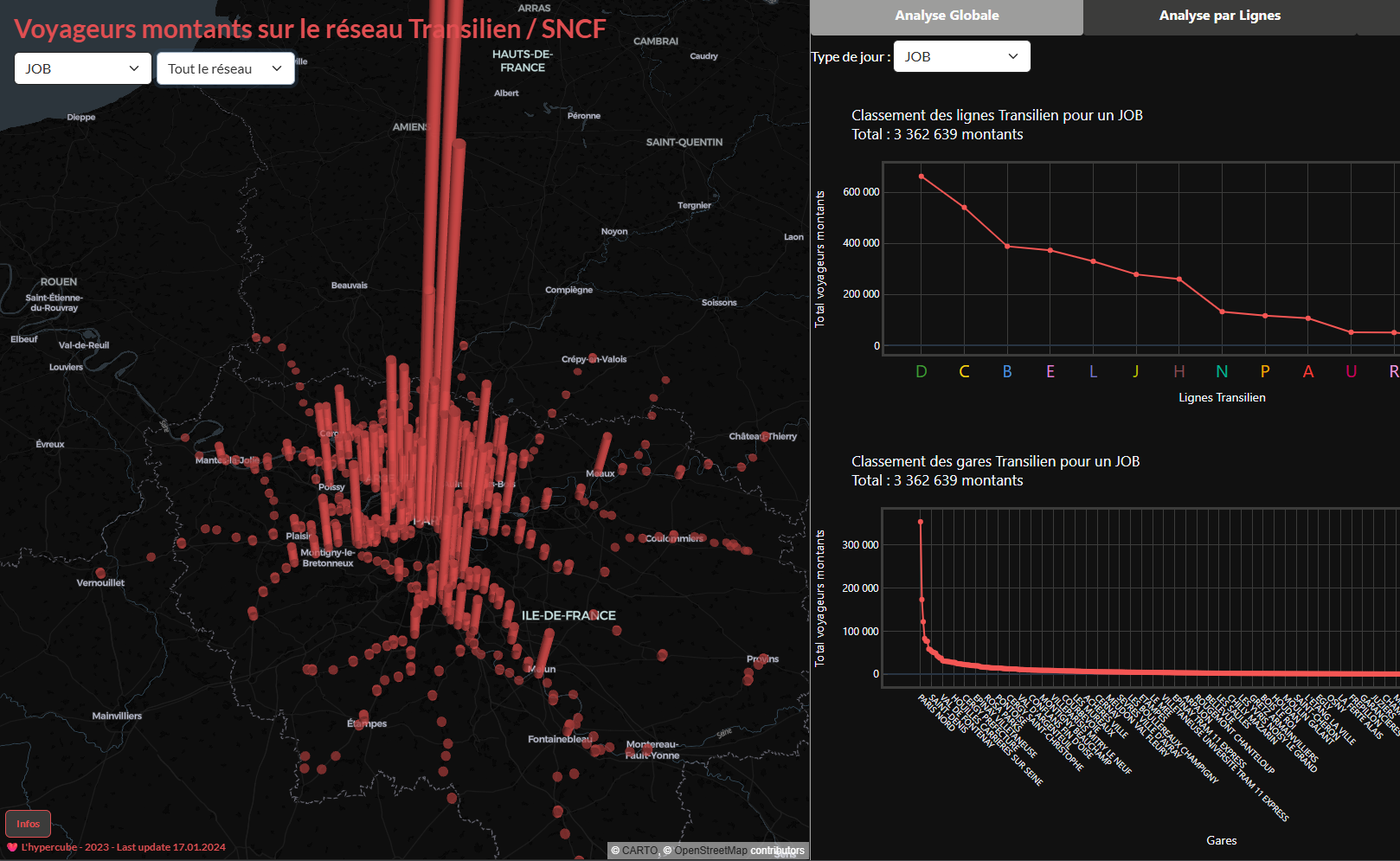
Access Frequ_idf_sncf